How To Make An Absorbance Spectrum On Excel

i: Using Excel for Graphical Assay of Data (Experiment)

Last updated
Save equally PDF

Page ID: 95875

Objectives

To learn to use Excel to explore a number of linear graphical relationships.

In several upcoming labs, a primary goal volition be to make up one's mind the mathematical relationship between two variable physical parameters. Graphs are useful tools that tin can elucidate such relationships. First, plotting a graph provides a visual paradigm of data and any trends therein. Second, via appropriate analysis, they provide united states of america with the ability to predict the results of any changes to the system.

An important technique in graphical analysis is the transformation of experimental data to produce a straight line. If there is a direct, linear relationship between two variable parameters, the data may be fitted to the equation of line with the familiar class \(y = mx + b\) through a technique known as linear regression. Here \(m\) represents the gradient of the line, and \(b\) represents the y-intercept, as shown in the figure beneath. This equation expresses the mathematical human relationship between the two variables plotted, and allows for the prediction of unknown values within the parameters.

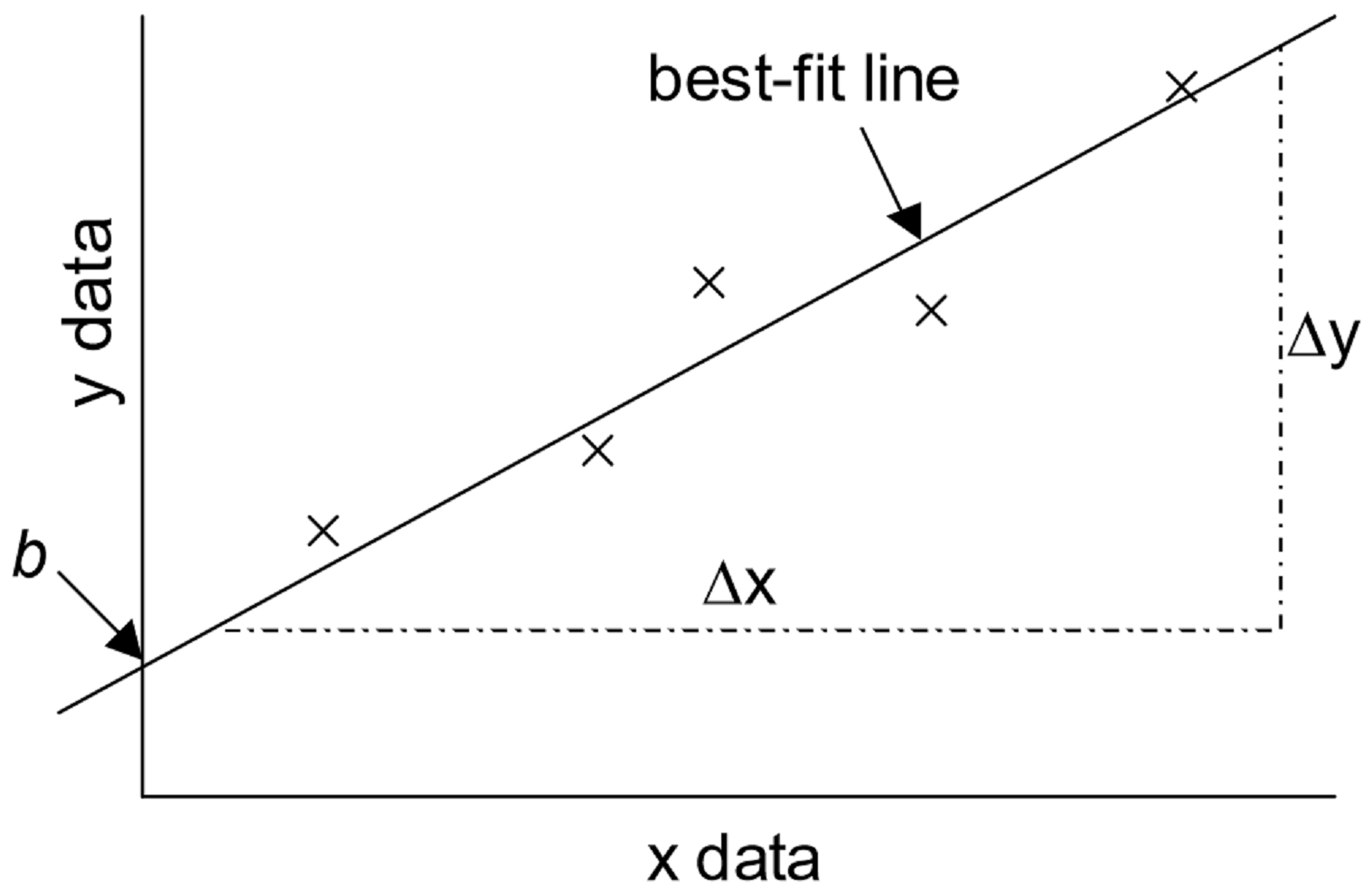
The equation for the best-fit line is

\[y = mx + b \characterization{1}\]

where

\[ \begin{align} b &= y\text{-intercept} \label{2} \\[5pt] m &= \text{gradient} \\[5pt] & = \dfrac{\Delta y}{\Delta x} \\[5pt] &= \dfrac{y_{2}-y_{one}}{x_{2}-x_{1}} \characterization{3} \end{marshal}\]

Computer spreadsheets are powerful tools for manipulating and graphing quantitative data. In this exercise, the spreadsheet plan Microsoft Excel^© volition be used for this purpose. In particular, students will acquire to use Excel in guild to explore a number of linear graphical relationships. Please notation that although Excel can fit curves to nonlinear data sets, this form of analysis is ordinarily not as accurate equally linear regression.

Procedure

Part ane: Unproblematic Linear Plot

Scenario: A certain experiment is designed to measure out the volume of 1 mole of helium gas at a variety of dissimilar temperatures, while keeping the gas pressure constant at 758 torr:

Temperature (K)	Book of Helium (L)
203	fourteen.iii
243	17.two
283	23.1
323	25.9
363	31.5

Launch the programme Microsoft Excel^© (2016 version, plant on all computers in all the figurer centers on campus). Go to the First push button (at the bottom left on the screen), and so click Programs, followed by Microsoft Excel^©.
Enter the above data into the outset two columns in the spreadsheet.

Reserve the first row for cavalcade labels.
The ten values must be entered to the left of the y values in the spreadsheet. Recall that the independent variable (the one that you, as the experimenter, accept control of) goes on the x-centrality while the dependent variable (the measured data) goes on the y-axis.

Highlight the set of data (not the cavalcade labels) that yous wish to plot (Figure 1).

Click on Insert > Recommended Charts followed by Scatter (Figure 2).

Choose the besprinkle graph that shows data points simply, with no connecting lines – the pick labeled Scatter with Only Markers (Figure 3).

You should now encounter a scatter plot on your Excel screen, which provides a preview of your graph (Figure four).

If all looks well, it is time to add together titles and label the axes of your graph (Figure 5).

Outset, click inside the chart.
Switch to the Pattern tab, and click Add Chart Chemical element > Chart Title > Above Chart
The graph should be given a meaningful, explanatory title that starts out "Y versus X followed by a description of your system.
Click on Centrality Titles (select Primary Horizontal Axis Title and Primary Vertical Centrality Title) to add together labels to the ten- and y-axes. Note that it is important to characterization axes with both the measurement and the units used.

To change the titles, click the text box for each title, highlight the text and blazon in your new title (Figure six).

Your side by side step is to add a trendline to the plotted data points. A trendline represents the best possible linear fit to your data. To practise this yous first need to "actuate" the graph. Do this by clicking on any one of the data points. When y'all do this, all the data points will appear highlighted.

Click the Chart Elements push button next to the upper-right corner of the chart.
Cheque the Trendline box.
Click More Options. This will brandish the selection shown in Effigy 7.
Notice that the Linear push button is already selected. Now select the Display Equation on Chart box and the Brandish R-squared value on Nautical chart box. And then click the Close push button.

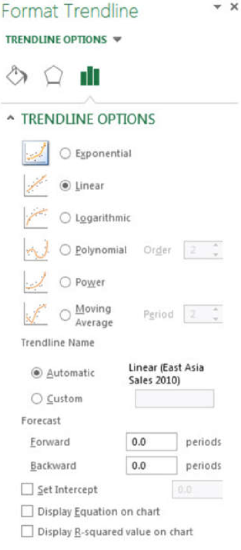
The equation that now appears on your graph is the equation of the fitted trendline. The R² value gives a measure of how well the data is fit by the equation. The closer the R² value is to 1, the meliorate the fit. Generally, R^two values of 0.95 or higher are considered good fits. Note that the program will e'er fit a trendline to the data no matter how skilful or awful the information is. You must guess the quality of the fit and the suitability of this type of fit to your data set.
Impress out a full-sized copy of your prepared graph and attach it to your report. And then record the following data on your written report:

the equation of the all-time-fit trendline to your data
the slope of the trendline
the y-intercept of the trendline
whether the fit of the line to the information is good or bad, and why.

Past graphing the five measured values, a relationship is established between gas book and temperature. The graph contains a visual representation of the relationship (the plot) and a mathematical expression of the human relationship (the equation). It can now be used to make sure predictions.

For case, suppose the 1 mole sample of helium gas is cooled until its volume is measured to be ten.five Fifty. You are asked to determine the gas temperature. Notation that the value 10.5 L falls outside the range of the plotted data. How tin you lot find the temperature if it doesn't fall between the known points? There are 2 ways to practice this.

Method (1): Extrapolate the trendline and approximate where the point on the line is.

Click on the Layout tab along the top menu, then Trendline > More Trendline Options.
In the department labeled Forecast enter a number in the box labeled Backward, since we want to extend the trendline the backward x direction. To determine what number to enter, await at your graph to see how far back along the x-centrality you need to become in order to cover the expanse where book = 10.v L. Later on entering a number, click Shut, and the line on your graph should now exist extended in the backward direction.
Now apply your graph to estimate the x value by envisioning a straight line down from y = 10.5 L to the 10-axis. Record this value on your report.

Method (2): Plug this value for book into the equation of the trendline and solve for the unknown temperature. Do this and record your respond on your study. Notation that this method is generally more than precise than extrapolating and "eyeballing" from the graph.

Part ii: Two Data Sets with Overlay

Scenario: In a certain experiment, a spectrophotometer is used to measure the light absorbance of several solutions containing different quantities of a red dye. The two sets of information nerveless are presented in the table beneath:

Data A		Data B
Amount of Dye (mol)	Absorbance (unitless)	Amount of Dye (mol)	Absorbance (unitless)
0.100	0.049	0.800	0.620
0.200	0.168	0.850	0.440
0.300	0.261	0.900	0.285
0.400	0.360	0.950	0.125
0.500	0.470
0.600	0.590
0.700	0.700
0.750	0.750

Y'all would like to see how these two sets of data relate to each other. To do this yous will have to place both sets of information, as contained relationships, on the same graph. Note that this procedure just works when you have the same axis values and magnitudes.

Enter this new data on a fresh page (Sheet 2) in Excel. Be sure to label your data columns A and B. Again, retrieve to enter the x values to the left of the y values.
Offset, plot Data A only every bit an XY Besprinkle plot (the same way you did with the data in Part 1). Fit a trendline to this information using linear regression, and obtain the equation of this line.
Now you need to add Data B to this graph.

Activate the graph by clicking on one of the plotted data points.
Right-click the nautical chart, and so choose Select Data. The Select Data Source box appears on the worksheet with the source data of the nautical chart.
Click the Add tab and type "Data B" for the Serial Name.
Click the little icon under Series X values, and then highlight the 10-axis values of Data B.
Printing enter, then repeat this procedure for the Series Y Values, highlighting the y-axis values of Data B. For each of these steps, y'all should meet a display similar to what is shown in Figure 8. Notation that slight differences may announced due to the version of Microsoft Excel^© installed on your computer.

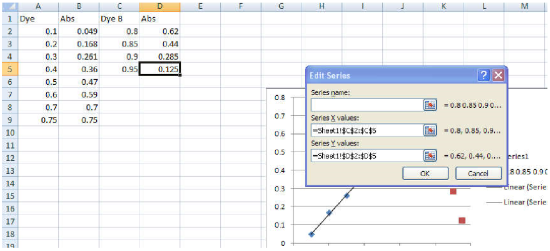
Click OK twice to return to the main Excel window.
At this point yous should see the new data points (labeled as Serial 2) every bit shown in Effigy 9. You tin can now independently analyze this dataset past inserting a trendline as before.

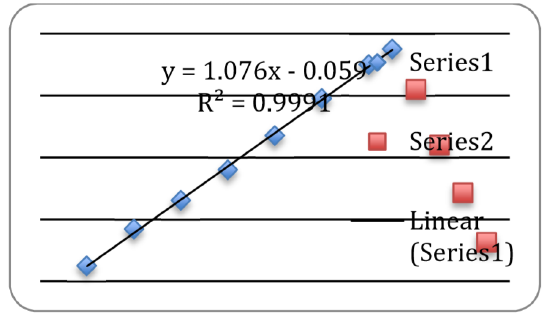
Impress out a full-sized copy of your prepared graph and attach it to your report. And so tape the following data on your report:

the equation of the all-time-fit trendline for Data A,
the equation of the all-time-fit trendline for Information B,
If these trendlines were extrapolated, they would intersect. Decide the values of x and y for the point of intersection using simultaneous equations.

Part 3: Statistical Analysis and Simple Scatter Plots

When many contained measurements are made for one variable, there is inevitably some scatter (noise) in the data. This is usually the upshot of random errors over which the experimenter has little control.

Scenario: Ten different students at two different colleges each measure the sulfate ion concentration in a sample of tap water:

College #i dataset	35.9 ppm	43.2 ppm	33.5 ppm	35.one ppm	32.8 ppm	37.6 ppm	31.9 ppm	36.half-dozen ppm	35.0 ppm	32.0 ppm
College #2 dataset	45.one ppm	34.2 ppm	36.8 ppm	31.0 ppm	40.vii ppm	29.6 ppm	35.4 ppm	32.5 ppm	43.five ppm	38.viii ppm

Simple statistical analyses of these datasets might include calculations of the hateful and median concentration, and the standard deviation. The hateful (\(\bar{x} \)) is simply the average value, defined as the sum (\(\Sigma\)) of each of the measurements (\(x_{i}\)) in a data gear up divided by the number of measurements (\(Northward\)):

\[ \bar{x}= \frac{ \sum x_{i}}{N} \characterization{6}\]

The median (\(M\)) is the midpoint value of a numerically ordered dataset, where half of the measurements are above the median and half are below. The median location of \(N\) measurements can exist plant using:

\[ G= \frac{N+1}{2} \label{7}\]

When \(Northward\) is an odd number, the formula yields a integer that represents the value respective to the median location in an ordered distribution of measurements. For case, in the set of numbers (3 1 5 4 ix ix 8) the median location is (seven + ane) / ii, or the 4 ^th value. When practical to the numerically ordered set (i 3 4 5 eight 9 ix), the number 5 is the four ^th value and is thus the median – three scores are to a higher place 5 and iii are beneath five. Note that if in that location were simply 6 numbers in the set (1 3 4 v viii 9), the median location is (half-dozen + one) / two, or the 3.v^th value. In this example the median is half-way between the three^rd and 4^th values in the ordered distribution, or 4.5.

Standard difference (\(south\)) is a measure of the variation in a dataset, and is defined as the square root of the sum of squares divided by the number of measurements minus one:

\[ due south= \sqrt{ \frac{ \sum (x_{i} - \bar{x})^{2}}{Northward-i}} \label{8} \]

Then to find \(south\), subtract each measurement from the hateful, square that result, add it to the results of each other deviation squared, divide that sum by the number of measurements minus one, and then accept the square root of this result. The larger this value is, the greater the variation in the data, and the lower the precision in the measurements.

While the mean, median and standard departure can be calculated by manus, information technology is oft more than convenient to utilise a computer or reckoner to determine these values. Microsoft Excel^©is specially well suited for such statistical analyses, especially on large datasets.

Enter the data acquired by the students from College #ane (only) into a single cavalcade of cells on a fresh folio (Sheet iv) in Excel. Then in whatever empty prison cell (usually one shut to the data cells), instruct the programme to perform the required functions on the data. To compute the mean or boilerplate of the information entered in cells a1 through a10, for example, yous must:

click the mouse in an empty jail cell
type "=average(a1:a10)"
and press render

To obtain the median y'all would instead type "=median(a1:a10)". To obtain the standard deviation you would instead blazon "=stdev(a1:a10)".

Tape on your report:

The Excel calculated mean, median and standard deviation for the Higher #1 dataset.
Equally an additional exercise, calculate the standard divergence of this dataset by paw, and compare it to the value obtained from the plan.

Rejecting Outliers

Practise all the measurements in the College #1 data set look equally skillful to you, or are at that place whatsoever values that exercise non seem to fit with the others? If so, are you lot allowed to reject these measurements?

Outliers are data points which lie far outside the range defined by the residue of the measurements and may skew your results to a great extent. If you decide that an outlier resulted from an obvious experimental error (e.k., you incorrectly read an instrument or prepared a solution), you may reject the point without hesitation. If, however, none of these errors is evident, yous must utilise circumspection in making your decision to keep or turn down a signal. One rough criterion for rejecting a data point is if it lies beyond ii standard deviations from the hateful or boilerplate.

Using the above criteria, determine if there are any outliers in the College #1 dataset.

Tape these outlier measurements (if any) on your written report.
Then, excluding the outliers, re-summate the mean, median and standard deviation of this information set up (apply Excel).

Rejecting data points cannot be done just considering you desire your results to look ameliorate. If y'all cull to reject an outlier for whatsoever reason, y'all must always include documentation in your lab report which conspicuously states:

that you did reject a point
which betoken you lot rejected
why you rejected it

Failure to disclose this could constitute scientific fraud.

Graphing a Scatter Plot

Different the linear plots created so far, a scatter plot simply shows the variation in measurements of a unmarried variable in a given dataset, i.east., it supplies a visual representation of the "noise" in the information. The information is plotted in a column, and in that location is no x-y dependence here (Effigy x). Note that datasets with a greater degree of scatter will take a higher standard departure and consist of less precise measurements than datasets with a small degree of besprinkle.

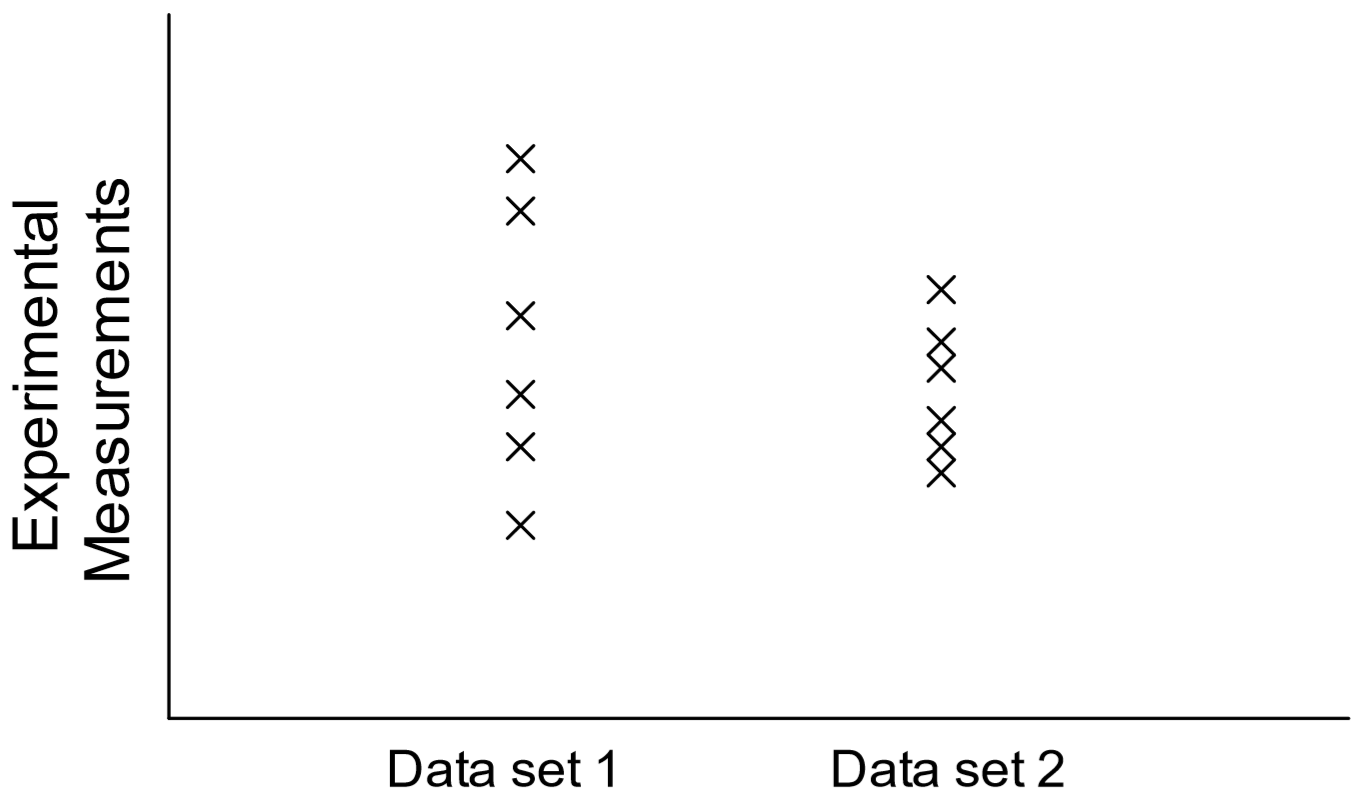
To obtain such a plot using Excel, all the ten values for each dataset must be identical. Thus, let the College #one information be assigned x = 1, and let x = 2 for all the Higher #2 information:

Measurements by Students from College #1		Measurements by Students from College #2
College ane	[\(\ce{SO4^{-ii}}\)] (ppm)	College 2	[\(\ce{SO4^{-2}}\)] (ppm)
one	35.9	2	45.1
1	43.2	2	34.2
i	33.5	2	36.eight
1	35.1	ii	31.0
ane	32.8	2	40.7
one	37.half-dozen	2	29.half dozen
1	31.9	two	35.iv
one	36.6	two	32.5
1	35.0	2	43.five
1	32.0	two	38.8

Enter the data as shown higher up into the get-go four columns of your spreadsheet.

Plot the Higher #ane dataset as an XY Scatter Plot.
Now add the Higher #2 dataset to this graph applying the same steps you used to create your earlier graph in the section "Two Data Sets with Overlay" (Part 2).
Add appropriate axis labels and a title. You may also want to adjust the ten-centrality and y-centrality scales to improve the final look of your graph.

Print out a total-sized copy of your prepared graph and adhere it to your report. And so record the post-obit information on your report:

Which dataset (Higher #1 or College #2) show the least scatter? The greater standard deviation? The more precise measurements?

Lab Study: Using Excel for Graphical Analysis of Information

Proper noun: ____________________________ Lab Partner: __None for this assignment__

Date: ________________________ Lab Section: __________________

Plough in the graphs you fabricated for ALL 3 parts in this assignment

For each graph make sure the post-obit components are in the printout:

Championship for the graph
Labels for x and y axes (along with appropriate units when applicable)
Line equation and R² when appropriate.

Role 1: Simple Linear Plot

Which set of data is plotted on the y-axis?
Which ready of data is plotted on the ten-centrality?
Record the following information:

The equation of the fitted trendline

The value of the slope of this line

The value of the y-intercept of this line

Is the fit of the trendline to your data good (circle one)? Yes / No. Explain why yous retrieve the line is a good fit to the data.

Determine the temperature (in 1000) of the gas in the common cold room when information technology has a measured volume of 10.five L using

a) Extrapolation and "eyeballing"

b) The equation of the trendline

Show your calculations for b) beneath.

Part 2: Two Data Sets and Overlay

Record the equations of the trendlines fitted to
- Data fix A:
- Data set B:
Perform a simultaneous equations calculation to determine the x and y values for the signal of intersection betwixt these lines. Show your work below.

Office three: Statistical Assay and Uncomplicated Scatter Plots

For the College #1 data set, record the following values (adamant using Excel):
- the mean \(\ce{SO4^{-2}}\) concentration
- the median \(\ce{SO4^{-2}}\) concentration
- the standard deviation in the data prepare
Calculate the standard departure in the Higher #1 data set by hand. Show all your work beneath. Proceed your work on an attached page if you lot require more infinite.

Are there whatsoever outliers in the College #1 data gear up (circumvolve one)? Yes / No
If yeah, which measurements are the outliers?
Prove the calculations yous used to place the outliers (or, if none, how you determined that there were none).

Re-summate the following values (using Excel) excluding the outliers:
- the hateful \(\ce{SO4^{-2}}\) concentration
- the median \(\ce{SO4^{-2}}\) concentration
- the standard deviation in the data set
Create a besprinkle plot showing both the College #one and College #two data. Attach a printout of your graph to this written report. Be certain that your axes are properly labeled, and that your graph has an appropriate title.
Examine your plotted data. Which data fix:

has the larger standard deviation?

contains the more than precise measurements?

Source: https://chem.libretexts.org/Ancillary_Materials/Laboratory_Experiments/Wet_Lab_Experiments/General_Chemistry_Labs/Online_Chemistry_Lab_Manual/Chem_11_Experiments/01:_Using_Excel_for_Graphical_Analysis_of_Data_%28Experiment%29

Posted by: nixharme1942.blogspot.com